Sabine’s Formula & The Birth of Modern Architectural Acoustics

Modern Architectural Acoustics’ Founding Father

Jump to Sabine’s Formula ↓

Wallace Clement Sabine, born in 1868, is considered the father of architectural acoustics. He attended Ohio State University where he studied physics. He later went to Harvard to pursue his graduate studies. After graduating, he joined Harvard as a faculty member teaching physics. When it came to the study of sound, Sabine never had any formal training. He became fascinated with how sound differed from one lecture hall to another. Along with his assistants, he began moving materials to different lecture halls to see what materials made the lecture halls sound better. Sabine and his assistants spent many nights moving materials and measuring sound waves; he and his team used an organ and a stop watch to measure the deterioration of sound as it passed through the lecture hall.

In one instance, Sabine discovered that one person sitting in a seat did as much to absorb sound as did six seat cushions. One night he even moved all the seat cushions from one lecture hall into another. He experimented with oriental rugs. After working late each night, Sabine and his assistants would restore the lecture halls back to their original form before classes began the next day. Sabine’s greatest achievement was to conclude that a relationship existed between the surface quantity of absorption materials placed on walls, seats, ceilings, and floors and the volume of the lecture hall. The more sound absorbing materials he used, the quieter the lecture became.

Sabine came up with a formula for determining the quality of sound in a lecture hall, auditorium, concert hall, or any other venue where people spoke or played music. In designing a venue, as just described, engineers and architects need to determine the sound reverberation time. Reverberation time is the time it takes an original sound to drop sixty decibels. Sabine chose sixty because the highest concert crescendo is about one hundred decibels. Dropping it to forty decibels would put it at normal room background noise.

Sabine came up with a formula that architects and engineers could use when designing a concert hall so they could achieve the best reverberation time for their particular venue.

Sabine found that 2 to 2.25 seconds was an optimal reverberation time for a concert hall, and around 1 second was optimal for a lecture hall. If a lecture hall had a reverberation time of more than one second, students would have to contend with multiple words at once.

The following are reverberation times for different concert halls.

Boston Symphony Hall: 1.8 seconds

Carnegie Hall in New York City: 1.7 seconds

Sabine’s Formula

Sabine’s formula is given by the following:

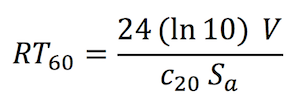
RT₆₀ is the reverberation time (to drop 60 dB)
V is the volume of the room
c₂₀ is the speed of sound at 20°C (room temperature)
Sa is the total absorption in sabins

The sabin unit has the same dimension as area (e.g. m²). A one square meter surface with an absorption coefficient of 0.75 would be considered 0.75 sabins. The absorption coefficient has a range of 0 to 1, where a coefficient of 0 indicates none of the sound is absorbed, and a coefficient of 1 indicates that 100% of it is absorbed.

Since we know the speed of sound at 20°C is 343 m/s, we can do a little math and reduce the formula to:

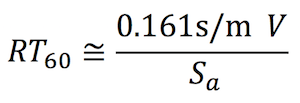
(Note that the factor 0.161 has the units seconds per meter; dimensional analysis on the equation will yield a time in seconds as the volume is measured in cubic meters and sabins in square meters).

Let us use this formula to calculate the reverberation time of a fictitious lecture hall. Let us say the hall has a 5-meter tall ceiling, is 20 meters wide and 10 meters deep. Let us also say that the absorption coefficient for the walls, ceiling, and floors is 0.3.

To use Sabine’s Formula, we’ll first need the volume:

The total absorption, in sabins, is the total area times the absorption coefficient. The total area in includes 4 walls, a ceiling, and a floor, which when multiplied by the absorption coefficient gives us the total absorption in sabins:

Let us use the dimensions of the room above, but specify different absorption coefficients for the different surfaces. Let us say the tile floor has a coefficient of 0.01, the ceiling a coefficient of 0.5, and the 4 walls a coefficient of 0.2.

The total absorption in Sabins becomes:

This is very close to one second, which is ideal for a lecture hall.

In the examples above, we used the metric system, but if we wanted to measure the room in feet, we would need to use the speed of sound in feet per second (1125 ft/s). Doing so would result in a different coefficient for Sabine’s formula:

(Note now the coefficient has the units s/ft. Here the sabin has the units of ft²and can be called the imperial sabin, as opposed the metric sabin used in the previous examples).

Conclusion

The sabin, named in honor of Wallace Sabine, is a unit of measure; one imperial sabin equals one square foot of 100% absorbing material, and one metric sabin equals one square meter of 100% absorbing material. Stemming from Sabine’s 19^th century work a new field of study was born. Today, computer programs incorporate Sabine’s formula to help engineers and architects model and design future concert and lecture halls around the globe.