Sound Pressure Math Made Easy
 Pretend for a moment you are Albert Einstein in 1905. You are working diligently on your soon-to-be five famous papers. Your ideas are about to turn the physics world on its head. In your papers you introduce the world for the first time to light quanta, later to be renamed photons. You propose a mathematical way to determine the size of atoms when their very existence was still in question. You provide an explanation for Brownian motion: that microscopic materials are moving in liquids because they are being bombarded by millions of molecules. You upend Newton’s belief of absolute space and time by proposing that time slows when velocity is increased. And most importantly, you introduce the world to the most eloquent formula in human history: E=mc2.
Pretend for a moment you are Albert Einstein in 1905. You are working diligently on your soon-to-be five famous papers. Your ideas are about to turn the physics world on its head. In your papers you introduce the world for the first time to light quanta, later to be renamed photons. You propose a mathematical way to determine the size of atoms when their very existence was still in question. You provide an explanation for Brownian motion: that microscopic materials are moving in liquids because they are being bombarded by millions of molecules. You upend Newton’s belief of absolute space and time by proposing that time slows when velocity is increased. And most importantly, you introduce the world to the most eloquent formula in human history: E=mc2.
In 1905 Einstein achieved more in one year than most physicists achieve in a lifetime. Years later he would rise to his pinnacle by giving the world a better understanding of gravity in his general theory of relativity. With all this great achievement, Einstein was plagued with an insecurity. For most of his adult life, Einstein complained that he didn’t know enough math. On his death bed on April 17, 1955 he half-jokingly said to his son Hans Albert, “If only I had more mathematics.” Before Einstein finished his General Theory of Relativity, mathematician Tullio Levi-Civita had to help Einstein with his tensor calculus.
When it comes to sound pressure our intention is not to let you suffer with the same math insecurities Einstein had. We want to make it easy for you to become a sound pressure mathematical genius. Below you find sound pressure math explained in an easy-to-learn fashion that will make you an authority on sound pressure math. Imagine if someone had laid out tensor calculus for Einstein this way. He may have finished his theory of relativity years earlier. Now let us dive into the wonderful world of pascals, decibels, and other units and see how they relate to sound.
Sound Pressure
When people talk of sound level, they usually refer to it in decibels. This may be when thinking about OSHA requirements, how loud a rock band is, jet engines, or town ordinances. So what are decibels? To answer that, let us first look at sound pressure. Sound is measured by changes in air pressure. The louder a sound is, the larger the change in air pressure is. The change here is the change from normal atmospheric pressure to the pressure disturbance made by the sound. This change in pressure can be measured by handheld devices or computers with special microphones.
Sound pressure is usually measured in pascals, which is an SI (metric) unit. A pascal (symbol Pa) is equal to a force of one newton per square meter. A pascal is “small” compared to some of the pressure units one may be familiar with, such as pounds per square inch. For instance, a tire pressure of 35 pounds per square inch is equal to about 241,000 pascals, or about 241 kilopascals. The smallest sound pressure a human ear can hear is 20 micropascals (0.000020 Pa). Writing this is scientific notation is convenient: 2.0×10-5 Pa. Remember this number – we will use this later as a reference.
The following table shows typical sound pressures of some recognizable things:
| Source | Sound Pressure (Pa) |
| Leaf rustling | 0.0000632 |
| Normal conversation | 0.01 |
| TV set at home | 0.02 |
| Passenger car as heard from roadside | 0.1 |
| Jack hammer | 2.0 |
| Jet engine as heard from 100 yards | 100 |
| Extremely loud rock band | 200 |
| Jet engine as heard from 1 yard | 630 |
As you can see, these numbers range from very small ones, with four zeroes after the decimal point, to numbers in the hundreds. To make working with this range of numbers more manageable, a special logarithmic scale has been devised.
The Decibel
To refresh your memory, a logarithm function is the inverse of the exponent function. Examples of exponents are:
102 = 100
103 = 1000
10-1 = 0.1
The inverse of this, the logarithm function (log10), is as follows:
log10(100) = 2
log10(1000) = 3
log10(0.1) = -1
The last equation can be spoken as, “the log base 10 of 0.1 equals -1.” The decibel unit (symbol dB) is a logarithmic unit expressing the ratio between two values. The decibel was named in honor of the famous scientist Alexander Graham Bell (1847-1922). When measuring sound, we use the following logarithmic formula to determine the sound pressure level (SPL) in decibels.
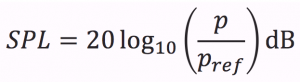
Here p is the sound pressure we are measuring, and Pref is our reference, the pressure of the smallest sound we can hear, 2.0×10-5 Pa (you remembered this, right?). For example, if we measure a sound pressure of 0.4 Pa, we can determine the SPL in dB:
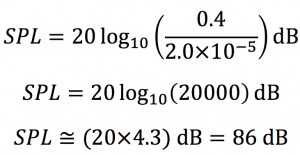
So a pressure change of 0.4 Pa equates to about 86 dB. In case you do not want to do the math on all of our examples above, here is that same table, now including sound pressure level.
| Source | Sound Pressure (Pa) | Sound Pressure Level (dB) |
| Leaf rustling | 0.0000632 | 10 |
| Normal conversation | 0.01 | 54 |
| TV set at home | 0.02 | 60 |
| Passenger car as heard from roadside | 0.1 | 74 |
| Jack hammer | 2.0 | 100 |
| Jet engine as heard from 100 yards | 100 | 134 |
| Extremely loud rock band | 200 | 140 |
| Jet engine as heard from 1 yard | 630 | 150 |
As you can see, we now have a range of numbers that seems more convenient – from 10 to 150 – instead of a range from a very, very, small number to a number in the hundreds. If you played around with the formula and plugged different pressure values in, you might notice that for every increase of 20 dB, the sound pressure has increased 10 times. That is because the scale with decibels is not linear, but rather logarithmic. That is a trade-off for using convenient numbers instead of the range from very small to very large ones.
 Fortunately for us, the devices that measure sound pressure level do the math for us, and give us the sound pressure level in decibels. Hopefully, this paper will give you a feel for the relationship of pressure and decibels, and an understanding of the logarithmic scale of decibels to aid you in your sound-related endeavors. We know Einstein would have enjoyed it!
Fortunately for us, the devices that measure sound pressure level do the math for us, and give us the sound pressure level in decibels. Hopefully, this paper will give you a feel for the relationship of pressure and decibels, and an understanding of the logarithmic scale of decibels to aid you in your sound-related endeavors. We know Einstein would have enjoyed it!
Get more information on Thermaxx Noise Insulation Jackets, or contact us.

Thermaxx Jackets
Thermaxx Jackets was founded over 25 years ago with a single purpose: to help our clients save energy with removable insulation blankets when traditional stay-in-place insulation is not practical. Our dedication to this purpose has resulted in a long list of customers who have saved money thanks to Thermaxx Jackets! Combining expertise in heat loss, wireless monitoring, insulation design, and several other disciplines, we’ve become the #1 provider and fabricator of removable insulation jackets and covers. The Thermaxx Sales and Service teams are experienced and trained to provide clients with the most timely and cost-effective solution.
Categories
- removable insulation
- thermaxx jackets
- energy savings
- savings
- energy efficiency
- safety
- pipe insulation
- energy
- case study
- insulation materials
- thermal insulation
- heat loss survey
- heat loss
- energy loss
- hot insulation
- fiberglass
- installation
- steam
- New York
- custom insulation
- NYC Case Study
- boiler
- university
- Connecticut
- reusable insulation






