The Doppler Effect Equation & Calculating Frequency Change

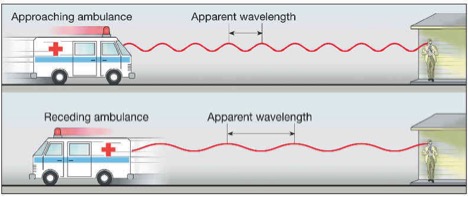
For a moment, close your eyes and pretend you are standing on a sidewalk and an ambulance is swiftly approaching your position. You listen as the ambulance draws near, and after it passes, the pitch, or frequency, of the siren seems to change.

In 1842 Christian Doppler hypothesized that sound frequencies change, relative to the observer, when emitted from a moving sound source. In 1845 Buys Ballot proved Doppler’s Hypothesis correct. As the ambulance approaches, the waves seem shorter and the frequency seems higher than when it moves away from you. When it’s moving away, the waves seem longer and the frequency seems lower. The Doppler Effect is illustrated in the cartoon above.

Calculating the Frequency Change

The formula for determining the frequency during this event is as follows:

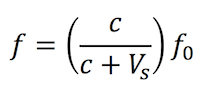
ƒ = observed frequency

c = speed of sound

Vs = velocity of source (negative if it’s moving toward the observer)

ƒ0 = emitted frequency of source

Suppose you are standing on the corner of 5^th Avenue and 34^th Street waiting for the light to change so you can cross the street. An approaching southbound ambulance is heading your way traveling at 35 miles per hour. If we know that the frequency of the ambulance siren is 700 Hz, we can calculate the frequency of what you hear:

c, the speed of sound, is 340.29 m/s

Vs, the velocity of the source, is 35 mi/h, or 15.6464 m/s

ƒ0, the frequency of the ambulance siren, is 700 Hz

Therefore,

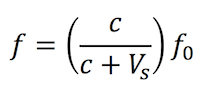becomes
(note: Vs is negative since the source is moving towards the observer)

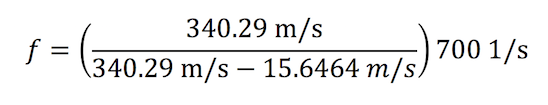
which reduces to:

ƒ ≈ 734 Hz

Once the ambulance passes, the frequency of the sound decreases, or sounds “lower”. The same calculation is performed to determine the observed frequency, except in this case Vs is positive:

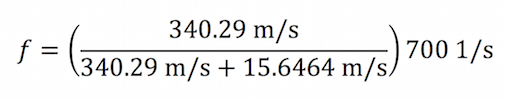
ƒ ≈ 669 Hz

A similar change in sound frequency is observed if the observer is moving towards a stationary sound source. In this case the formula is:

Where Vr is the velocity of the receiver, or observer. (note: this is negative if the observer is moving away from the source).

So, as an example, if you are driving your boat at 50 knots towards a buoy with a foghorn emitting a 400 Hz signal, the frequency of the sound you hear would be:

Where is Vr is 50 knots, or 25.722 m/s

ƒ ≈ 430 Hz

We can also calculate the observed frequency if both the source sound and the observer are moving towards each other. In this case, the formula is:

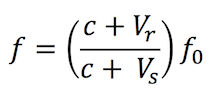
Now pretend that you and your friends are sitting on top of a tour bus heading southbound on 7^th Avenue at 30 miles per hour. That same ambulance is heading towards your bus at 28 miles per hour. We can now calculate the frequency of what you hear:

Vr, the velocity of the source, is 30 mi/h, or 13.4112 m/s
Vs, the velocity of the source, is 28 mi/h, or 12.51712 m/s

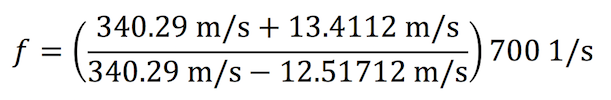
ƒ ≈ 755 Hz

Conclusion

Sound waves seem to compress or elongate with moving sound source. Moving forward causing the waves in front to seemingly compress and waves in back to seemingly elongate. The sound coming from an approaching ambulance siren will have a higher pitch than when it’s moving away from you. This happens to be a very practical by-product of sound physics. We need to be able to differentiate between an approaching ambulance and a retreating one so we can take the necessary precautions like pulling our vehicles over to the side of the road.

Learn about Thermaxx sound insulation, or contact us.