The Newton-Laplace Equation & Speed of Sound

In order to determine the speed of sound in a particular medium, we need to know the medium’s elastic properties and its density. A medium’s elastic properties determine whether or not the medium will deform or lose its shape due to external forces. Sound travels faster in mediums with high elasticity and minimal deformity – like steel. Sound travels more slowly in less rigid mediums that deform easily – like rubber. Sound travels more slowly in mediums with greater density.

Sir Isaac Newton proposed a simple formula for calculating the speed of sound. Years later Pierre-Simon Laplace would revise Newton’s formula and the new formula would be called the Newton-Laplace Equation.

Developing the Equation

In the latter half of the 17^th century, Sir Isaac Newton published his famous work Principia Mathematica. Newton thought that he correctly predicted the speed of sound though a medium: solid, liquid, or gas. If he knew the density of the medium and pressure acting on the sound wave, he believed he could ascertain the speed of sound by calculating the square root of the pressure divided by the medium’s density:

c = speed of sound
P = pressure acting on the sound
p = density of the medium

On page 301 in The Principia Mathematica Newton states “in mediums of equal density and elastic force (the medium’s pressure in Pascals, or Newtons over area measured in meters squared), all pulses are equally swift”. In the earth’s atmosphere at sea level all sound will consistently travel at the same velocity. The same goes for other mediums like homogenius liquids and solids.

Pierre-Simon Laplace

Newton further states that “if density or the elastic force of the medium were increased, then, because the motive force is increased in the ratio of the elastic force, and the matter to be moved is increased in the ratio of density, the time which is necessary for producing the same motion as before will be increased in the subduplicate ratio of the density, and will be diminished in the in the subduplicate ratio of the elastic force.” Ultimately, Newton is saying that if the medium’s density increases, the sound velocity slows and inversely if the medium’s pressure increases the sound velocity accelerates.

Later in the same century, French mathematician Pierre-Simon Laplace saw the flaw in Newton’s thinking and ultimately corrected Newton’s formula. He expanded Newton’s equation to include the idea that the process is not isothermic as Newton had thought, but it is adiabatic. Laplace slightly revised Newton’s formula by adding gamma to Newton’s pressure component. Laplace correction:
Newton’s formula neglected the influence of heat on the speed of sound. Laplace made this correction. Laplace multiplied the gamma (heat component) x the pressure. Experimentation proved that Newton’s results were wrong. Results from Newton’s equations fell short of what really took place. Laplace’s fix hit the mark. A new equation was born: The Newton-Laplace Equations. Laplace shorted the equation by having K = gamma × pressure. K refers to the elastic bulk modulus. The formula is called the Newton-Laplace equation:

Putting the Equation to Work

Determining Bulk Modulus

The speed of sound in sea level atmosphere at 20° Celsius is 343.21 m/s. Since we know the density of air at sea level is 1.2041 kg/m³. We can solve for K.

Squaring both sides leaves (rounding):

or

and finally:

Determining Density

The speed of sound in fresh water 1,428 m/s. Water’s elastic bulk modulus is 2.2 × 10⁹ Pa. Knowing these two values, we can confirm water’s density.

Squaring both sides leaves:

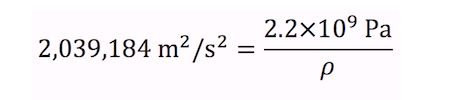
or

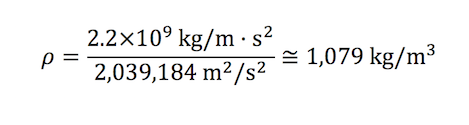
Determining the Speed of Sound

The density of cold-rolled steel is 7861 kg/m³. Its elastic bulk modulus is 159 GPa. With these two values, we can calculate the speed of sound through cold-rolled steel.

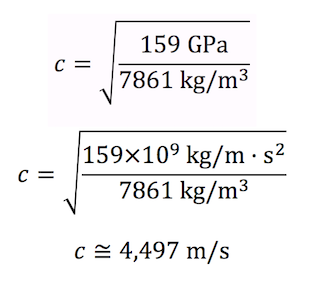
Conclusion

If we know a particular medium’s elastic bulk modulus and its density, we can calculate the speed of sound traveling through it. Sound travels faster in mediums with higher elasticity like steel and iron as shown in the steel equation above. In mediums like rubber and fiberglass sound travels slower. These mediums easily deform when forces are applied. We can conclude that the sound wave is being attenuated and or absorbed when passing through solids that are easily deformed when a force is applied. The stiffer and less rigid the medium the faster sound will travel through it.

Get more information about Thermaxx’s Sound Insulation or contact us!