Riding A Sound Wave
This article was written by Frank Kaputa and Mike Bannon of Thermaxx Jackets
Pretend for moment that you are riding a sound wave just emitted from oil refinery compressor. You are traveling on a wave in the air at atmospheric pressure and you slam into an acoustic wall consisting of fiberglass, recycled tires, and mass loaded vinyl. Picture what it would be like.
Part of you would be reflected back and the rest would enter into the acoustic wall’s first layer – needled fiberglass. Part of you that was reflected back would be a shadow of your original self – much weaker. Your wavelength, frequency and speed would remain the same, however, but your amplitude (energy) would be less. The part of you that in thrust into the acoustic wall would have the same frequency and wavelength you possessed before entering the new medium, however, your amplitude would be less and your speed, according to the Newton-Laplace equation, would be slower.
As you enter needled fiberglass, the first layer of the acoustic wall, the material is easily deformed. Picture yourself punching and kicking your way through it. As you punch and kick you begin to lose energy and heat is being generated by your body. Your heat is transferred into the surrounding colder material. This is Newton’s Second Law of Thermodynamics: heat always transfers from hot to cold and never vice versa.
Then you slam into the ½ inch of Silent Tread. Silent Tread is old tires chopped up and fused together. This material is denser than the fiberglass so you have to put up more of a fight. You are losing more energy and still giving off heat. Then you slam into the ½ inch of mass loaded vinyl. This material is higher density than the Silent Tread. Your kicking and punching have slowed tremendously as well as the heat you are giving off. You finally break through and you are free. You are not the same as when you entered the acoustic wall. You are much weaker than before. With no solid barriers in site, you will travel through the atmosphere and finally end when the atmospheric pressures are done with you.
Let’s explore what is actually happening when the wave enters into the three different sound absorbing materials. The wave is energy. When the sound enters into the needled fiberglass the energy excites the atoms. We know from Newton’s First Law of Thermodynamics that energy cannot be made or destroyed it can only be transformed into another form of energy. The sound wave travels into fiberglass. The wave is not punching or kicking but it is struggling to get through material.
Acoustic Impedance
When a sound wave encounters an acoustic wall like the one we described above, part of the wave is reflected back and the rest is transferred through the material. Depending on the makeup of barrier, whether it hard, soft, or somewhere in between, we can use a variety of formulas to determine how much of the sound wave is reflected and how much is transferred into the medium.
How much of the wave is reflected and how much is transferred into the medium depends on the physical properties of each medium. In this case, these include the properties of the air and the properties of the acoustic wall. Using these properties, we can find the impedance of a material, or the opposition to the flow of sound. To calculate the impedance, we simply multiply the density of the medium by the speed of sound in the medium.
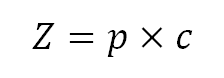
Z is the impedance, measured in pascal-seconds per cubic meter (Pa·s/m3)
p is the density, measured in kilograms per cubic meter (kg/m3)
c is the speed of sound in the medium, measured in meters per second (m/s)
Alternately, acoustic impedance can also be calculated using measurements called acoustic pressure and volume flow rate. Acoustic pressure is pressure exerted on a medium by nearby sound waves, and volume flow rate is the amount of sound moving within a medium per unit of time. To get the impedance, we simply divide the acoustic pressure by the volume flow rate for a specific medium, as seen below.
Z is the impedance, measured in pascal seconds per cubic meter (Pa·s/m3)
p is the acoustic pressure, measured in Pascals (Pa)
Q is the volume flow rate, measured in cubic meters per second (m3/s)
As the acoustic pressure applied to the boundary of a medium increases, the volume flow rate of sound within that medium also increases. Furthermore, for media with varying impedance values, equivalent acoustic pressures will result in different volume flow rates.
Although the acoustic impedance can be represented as a single number, it is actually a combination of two specific properties of the medium: acoustic resistance and acoustic reactance. Acoustic resistance is the opposition to the flow of sound waves due to energy losses of friction, whereas acoustic reactance is the opposition due to the inertia and elasticity of the medium. However, since both properties describe opposition to sound, they are commonly combined into a single impedance value.
Transmittance and Reflectance
Once we have calculated the impedance, we can use it to find out how much of the sound wave is reflected and how much is transmitted when traveling between media. As mentioned earlier, the amount of a wave transmitted and reflected depends on the physical properties of the two different media, represented by the impedance. The formulas for reflectance and transmittance are relatively simple, and are described below.
If a wave with amplitude ξ1 in medium 1 encounters a boundary with medium 2, the amplitudes of the reflected wave is given by
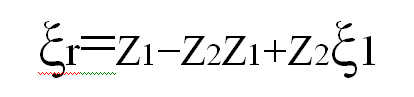
and the amplitude of the wave transmitted into medium 2 is given by
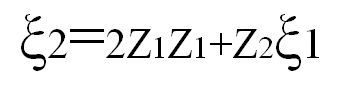
Snell’s Law
When a wave hits a medium, part of the wave is transferred into the medium at a refracted angle. We can calculate the angle by using Snell’s law. Snell’s law, as seen in the formula below, depends on two values for each medium: the speed of sound in the medium (c), and the angle the wave makes with the surface of the medium (θ). The speed of sound in the medium depends on the medium’s elasticity and density. A medium with a greater density, for example, will conduct sound at a lower velocity than a medium with a lower density.
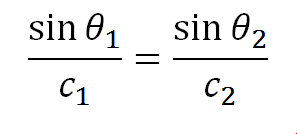
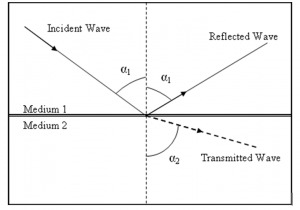
In the diagram above, Medium 1 conducts sound at a higher velocity than does Medium 2.
As seen in the diagram above, sound moving from a slower medium to a faster medium will be refracted at a smaller angle to the surface, whereas sound moving from a faster medium to a slower medium would be refracted at a larger angle to the surface. (Note: all parts of the wave that are not refracted will reflect off the surface at the same angle)
Acoustic Attenuation
Let’s go back to our story above where you are riding a sound wave and you were kicking, punching and getting tired losing energy. Attenuation is the amount of energy lost during your kicking and punching, or more accurately, when sound wave passes through a different medium, attenuation is the energy lost due to the elasticity and viscosity of the material. Elasticity is the material’s reaction to stress. Materials that easily deform when stress is applied make for good sound attenuating materials. Viscosity, on the other hand, is the “thickness” of a material, or its resistance to flow. The word “viscoelasticity” can be used describe the combined effects of both properties.
Although attenuation in its conceptual view is relatively straightforward, calculating the attenuation within a material can be much more complex. Experimental and field measurements show that an acoustic attenuation coefficient for a wide range of viscoelastic materials, such as soft tissue, polymers, soil and porous rock, can be expressed as the following power law.

Where:
ω is the angular frequency
P the pressure
Δχ is the wave propagation distance
α(ω) is the attenuation coefficient
αO and frequency dependent exponent are real non-negative material parameters obtained by fitting experimental data (η ranges from 0 to 2)
Acoustic attenuation in water, many metals, and crystalline materials are frequency-squared dependent (η=2). In contrast, the exponent η of sediment, soil and rock is about 1, and the exponent η of most soft tissues is between 1 and 2.
In recent decades, increasing attention and efforts are focused on developing accurate models to describe general power law frequency-dependent acoustic attenuation. Most of these recent frequency-dependent models are established via the analysis of the complex wave number and are then extended to transient wave propagation. The multiple relaxation model considers the power law viscosity underlying different molecular relaxation processes. On the other hand, acoustic wave equations based on fractional derivative viscoelastic models are also applied to describe the power law frequency-dependent acoustic attenuation.
The phenomenon of attenuation obeying a frequency power-law may be described using a causal wave equation, derived from a fractional constitutive equation between stress and strain. This wave equation incorporates fractional time derivatives:
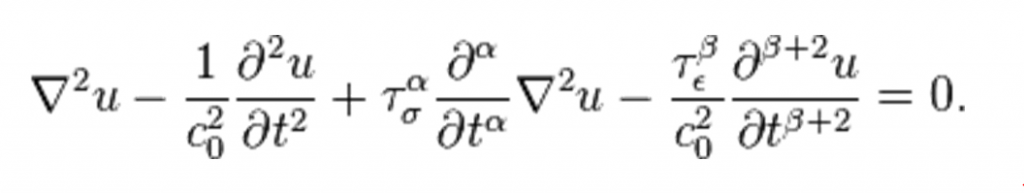
Categories
- removable insulation
- thermaxx jackets
- energy savings
- savings
- energy efficiency
- safety
- pipe insulation
- energy
- case study
- insulation materials
- thermal insulation
- heat loss survey
- heat loss
- energy loss
- hot insulation
- fiberglass
- installation
- steam
- New York
- custom insulation
- NYC Case Study
- boiler
- university
- Connecticut
- reusable insulation








